Grund- und Dimensionsvektorraum, Axiome, Eigenschaften

A Vektorraum Es ist ein nicht mittelscheifter Satz V= oder, v, W,…, deren Elemente sind Vektoren. Mit ihnen werden einige wichtige Operationen durchgeführt, unter denen sich die folgenden herausstechen:

- Summe zwischen zwei Vektoren U + v infolge z, das gehört zum Ganzen V.

- Multiplikation einer reellen Zahl α mit einem Vektor v: α v Das gibt einen anderen Vektor Und was gehört zu V.

Künstlerische Vision eines Vektorraums. Quelle: Pixabay

Um einen Vektor zu bezeichnen, verwenden wir BOLD (v Es ist ein Vektor) und für die Skalare oder Zahlen griechische Buchstaben (α ist eine Zahl).

[TOC]

Axiome und Eigenschaften

Um ein Vektorraum zu sein, müssen die nächsten acht Axiome erfüllt sein:

1-Konvartierbarkeit: oder +v = v +oder

2-Transitivität: (oder + v) + W = oder + ( v + W)

3-Existenz des Nullvektors 0 so dass 0 + v = v

4-Existenz des Gegenteils: das Gegenteil von v Ist (-v) , Angesichts dessen v + (-v) = 0

5-Produktverteilung in Bezug auf die Vektorsumme: α ( oder + v ) = αoder +αv

6-Produktverteilung in Bezug auf die Skalarsumme: (α + β)v = αv +βv

7-Assoziativität des Skalarprodukts: α (β v) = (α β)v

8-die Zahl 1 Es ist das neutrale Element seit: 1v = v

Beispiele für Vektorräume

Beispiel 1

Vektoren in der Ebene (R²) sind ein Beispiel für den Vektorraum. Ein Vektor in der Ebene ist ein geometrisches Objekt, das Größe und Richtung aufweist. Es wird durch ein orientiertes Segment dargestellt, das zu dieser Ebene gehört und mit einer Größe proportional zu seiner Größe.

Die Summe von zwei Vektoren in der Ebene kann als geometrischer Betrieb des zweiten Vektors nach dem ersten definiert werden. Das Ergebnis der Summe ist das orientierte Segment, das vom Ursprung des ersten beginnt und die Spitze der zweiten erreicht.

In der Abbildung kann beachtet werden, dass die Summe in r² kommutativ ist.

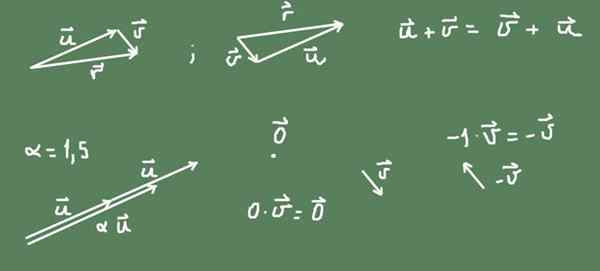Figur 2. Vektoren in der Ebene bilden Vektorraum. Quelle: Selbst gemacht.

Das Produkt einer α -Zahl wird auch durch einen Vektor definiert. Wenn die Zahl positiv ist, wird die ursprüngliche Vektoradresse beibehalten und die Größe ist α mal der ursprüngliche Vektor. Wenn die Zahl negativ ist, ist die Adresse das Gegenteil und die resultierende Vektorgröße ist der absolute Wert der Zahl.

Der Vektor lehnt einen Vektor ab v Ist -v = (-1) v.

Der Nullvektor ist ein Punkt in der R² -Ebene, und die Nullzahl durch einen Vektor führt zum Nullvektor.

Alle gesagt sind in Abbildung 2 dargestellt.

Beispiel 2

Satz P Von allen Polynomen, die weniger als oder gleich zwei, einschließlich der Nullgrad, bilden sie einen Satz, der alle Axiome eines Vektorraums entspricht.

Es kann Ihnen dienen: gegenseitig ausschließliche Ereignisse: Eigenschaften und Beispiele

Seien Sie das Polynom p (x) = a x² + b x + c y q (x) = d x² + e x + f

Die Summe von zwei Polynomen ist definiert: p (x) + q (x) = (a + d) x² + (b + e) ​​x + (c + f)

Die Summe der Polynome, die zum Ganzen gehören P Es ist kommutativ und transitiv.

Das Nullpolynom, das zum Ganzen gehört P Es ist eines, das alle seine Koeffizienten entspricht: Null:

0 (x) = 0 x² + 0 x + 0

Die Summe eines α -Skalars wird durch ein Polynom definiert, wie z

Das entgegengesetzte Polynom von p (x) ist -p (x) = (-1) p (x).

Aus all den oben genannten folgt es, dass der Satz P Von allen Polynomen, die weniger als oder gleich zwei sind, ist es ein Vektorraum.

Beispiel 3

Satz M Von allen Matrizen von M -Zeilen x n Spalten, deren Elemente reelle Zahlen sind.

Beispiel 4

Der Satz F von kontinuierlichen Funktionen realer Variable, bildet einen Vektorraum, da die Summe von zwei Funktionen definiert werden kann, die Multiplikation eines Skalars durch eine Funktion, die Nullfunktion und die symmetrische Funktion. Sie erfüllen auch die Axiome, die einen Vektorraum charakterisieren.

Basis und Dimension eines Vektorraums

Base

Eine Reihe von linear unabhängigen Vektoren wird als Grundlage eines Vektorraums definiert, so dass aus einer linearen Kombination von ihnen jeder Vektor dieses Vektorraums erzeugt werden kann.

Linear kombiniert zwei oder mehr Vektoren besteht darin, Vektoren mit einem Skalar zu vervielfachen und sie dann vektorisch hinzuzufügen.

Beispielsweise wird im Vektorraum des Vektors in drei Abmessungen, die durch r³ gebildet werden, die kanonische Basis, die durch die Einheitsvektoren (von Größe 1) definiert ist (von Größe 1) Yo, J, k.

Wo Yo = (1, 0, 0); J = (0, 1, 0); k = (0, 0, 1). Dies sind kartesische oder kanonische Vektoren.

Jeder Vektor V Die Zugehörigkeit zu R³ ist geschrieben als V = a Yo + B J + C k, Das ist eine lineare Kombination von Basisvektoren Yo, J, k. Skalare oder Zahlen A, B, C werden als kartesische Komponenten von bezeichnet V.

Es wird auch gesagt, dass die Basisvektoren eines Vektorraums einen Satz Vektorraum bilden.

Abmessungen

Die Dimension eines Vektorraums ist die Kardinalzahl einer Vektorbasis für den Raum; Das heißt, die Anzahl der Vektoren, die diese Basis ausmachen.

Dieser Kardinal ist die maximale Anzahl linear unabhängiger Vektoren dieses Vektorraums und gleichzeitig die minimale Anzahl von Vektoren, die einen generierenden Satz von diesem Raum bilden.

Kann Ihnen dienen: Statistische Bevölkerung: Konzept, Typen, Beispiele

Die Grundlagen eines Vektorraums sind nicht einzigartig, aber alle Basen desselben Vektorraums haben die gleiche Dimension.

Vektor -Unterraum

Ein Vektor -Unterraum eines Vektorraums V ist eine Untergruppe von V, in der die gleichen Operationen wie in V definiert sind und alle Axiome des Vektorraums erfüllt. Daher wird der Unterraum auch ein Vektorraum sein.

Beispiel für den Vektor -Unterraum sind die Vektoren, die zur XY -Ebene gehören. Dieser Unterraum ist eine Untergruppe eines Vektorraums der Dimensionalität größer als der Satz von Vektoren, die zum dreidimensionalen Raum XYZ gehören.

Ein weiteres Beispiel für den Vektor -Unterraum S1 des Vektorraums ist durch alle 2 × 2 -Matrizen mit realen Elementen, die unten definiert sind:

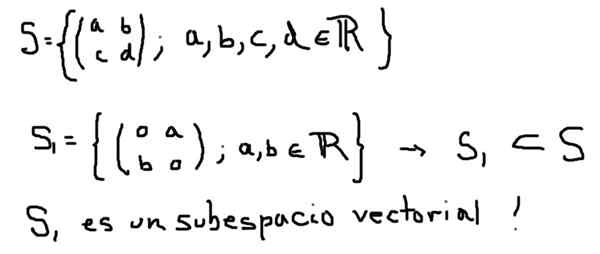
Auf der anderen Seite definiert S2, obwohl es sich um eine Untergruppe von S handelt, es bildet kein Vektor -Unterraum:

Gelöste Übungen

-Übung 1

Sei die Vektoren V1= (1, 1, 0); V2= (0, 2, 1) und V3= (0, 0, 3) in r³.

a) Beweisen Sie, dass sie linear unabhängig sind.

b) Beweisen Sie, dass sie eine Basis in R³ bilden, da jede Liste (x, y, z) als lineare Kombination aus V1, V2, V3 geschrieben werden kann.

c) Finden Sie die Komponenten der Liste V = (-3,5,4) an der Basis V1, V2, V3.

Lösung

Das Kriterium zur Nachweis der linearen Unabhängigkeit besteht darin, den folgenden Satz von Gleichungen in α, β und γ zu ermitteln

α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)

Falls die einzige Lösung für dieses System α = β = γ = 0 ist, dann sind die Vektoren linear unabhängig, sonst sind sie nicht.

Um die Werte von α, β und γ zu erreichen, schlagen wir das folgende Gleichungssystem vor:

α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0

α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0

α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0

Die erste führt zu α = 0, dem zweiten α = -2 ∙ β, aber als α = 0, dann β = 0. Die dritte Gleichung impliziert, dass γ = (-1/3) β, aber als β = 0, dann γ = 0.

Antwort auf

Es wird der Schluss gezogen, dass es sich um eine Reihe von linear unabhängigen Vektoren in R³ handelt .

Antwort b

Schreiben wir nun die Liste (x, y, z) als lineare Kombination aus V1, V2, V3.

(x, y, z) = α V1 + β V2 + γ V3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)

α ∙ 1 + β ∙ 0 + γ ∙ 0 = x

α ∙ 1 + β ∙ 2 + γ ∙ 0 = y

Es kann Ihnen dienen: Tukey -Test: Was ist bei Beispiels gelöstes Training

α ∙ 0 + β ∙ 1 + γ ∙ 3 = z

Wo du hast:

α = x

α + 2 β = y

β + 3 γ = z

Der erste zeigt α = x, das zweite β = (y-x)/2 und das dritte γ = (z-y/2 +x/2)/3 an. Auf diese Weise haben wir die Generatoren von α, β und γ einer beliebigen R³ -Liste gefunden 

Antwort c

Lassen Sie uns die Komponenten der Liste finden V = (-3,5,4) an der Basis V1, V2, V3.

Wir ersetzen die entsprechenden Werte in den oben gefundenen Ausdrücken für die Generatoren.

In diesem Fall haben wir: α = -3; β = (5-(-3))/2 = 4; γ = (4- 5/2 +(- 3)/2)/3 = 0

Das ist:

(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)

Endlich:

V = -3 V1 + 4 V2 + 0 V3

Wir schließen daraus V1, v2, v3 Sie bilden eine Basis im Vektorraum R³ von Dimension 3.

-Übung 2

Express Polynom p (t) = t² + 4t -3 als lineare Kombination von p1 (t) = t² -2t + 5, p2 (t) = 2t² -3t und p3 (t) = t + 3.

Lösung

P (t) = x p1 (t) + und p2 (t) + z p3 (t)

wo die Zahlen x, y, z bestimmt werden müssen.

Durch Multiplizieren und Gruppieren mit dem gleichen Abschluss in T wird es erhalten:

T² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)

Dies führt uns zu dem folgenden Gleichungssystem:

x + 2y = 1

-2x -3y + z = 4

5x + 3z = -3

Die Lösungen dieses Gleichungssystems sind:

x = -3, y = 2, z = 4.

Das ist:

P (t) = -3 p1 (t) + 2 p2 (t) + 4 p3 (t)

-Übung 3

Zeigen Sie diese Vektoren V1= (1, 0, -1, 2); V2= (1, 1, 0, 1) und V3= (2, 1, -1, 1) von r⁴ sind linear unabhängig.

Lösung

Wir kombinieren die drei Vektoren linear V1, V2, V3 Und wir fordern, dass die Kombination das Nullelement von R⁴ hinzufügt

Zu V1 + B V2 + C V3 = 0

Das heißt,

A (1, 0, -1, 2) + B (1, 1, 0, 1) + C (2, 1, -1, 1) = (0, 0, 0, 0)

Dies führt uns zu dem folgenden Gleichungssystem:

A + b + 2 c = 0

B + C = 0

-A - c = 0

2 A + B + C = 0

Subtrahieren Sie die erste und vierte, die wir haben: -a + c = 0 Was impliziert a = c.

Aber wenn wir uns die dritte Gleichung ansehen, müssen wir = -c. Der einzige Weg, um a = c = (-c) zu treffen, besteht darin, dass C 0 beträgt und daher auch 0 ist.

A = c = 0

Wenn wir dieses Ergebnis in der ersten Gleichung ersetzen, schließen wir, dass b = 0.

Schließlich a = b = c = 0, daher kann der Schluss gezogen werden, dass die Vektoren v1, v2 und v3 linear unabhängig sind.

Verweise

1. Lipschutz, s. 1993. Lineare Algebra. Zweite Ausgabe. McGraw - Hill. 167 - 198.